Q9. The adjacent sides of a parallelogram are 10 m and 8 m. If the distance between the longer sides is 4 m, find the distance between the shorter sides.

Sol.
ABCD is a parallelogram with side AB = 10 m.
And corresponding altitude DL =4 m.
The adjacent side is BC = 8 m.
And the corresponding altitude is DM.
We know that area of a parallelogram = Base × Height
$$ \Rightarrow \quad AB \times DL= BC \times DM $$ $$ \Rightarrow \quad 10 \times 4= 8 \times DM $$ $$ \Rightarrow \quad DM = \frac {10 \times 4}{8} $$ $$ \Rightarrow \quad DM = 5 \text { m} $$ Hence, the distance between the shorter sides is 5 m.
Q10. The base of a parallelogram is twice its height. If the area of the parallelogram is 512 sq cm, find the base and height.
Sol.

Let’s assume that height of the parallelogram be x cm.
Then given that base of the parallelogram is 2x cm. \begin{array}{l} \text {Also given that area of the parallelogram }=512 \text { cm}^{2} \\ \text {We know that area of a parallelogram }= \text {Base} \times \text {Height} \\ \Rightarrow \quad 512= 2x \times x \\ \Rightarrow \quad 2 x^{2}= 512\\ \Rightarrow \quad x^{2}= \frac {512}{2}\\ \Rightarrow \quad x^{2}= 256 \\ \Rightarrow \quad x= \sqrt {16 \times 16} \\ \Rightarrow \quad x= 16 \text { cm} \\ \text {Hence height of parallelogram }=x=16 \text { cm} \\ \text {And so base of the parallelogram }=2x=2 \times 16=32 \text { cm} \end{array}Q11. Find the area of a rhombus having each side equal to 15 cm and one of whose diagonals is 24 cm.
Sol.

Let ABCD be the rhombus where diagonals intersect at O.
Given that side of rhombus =15 cm.
And the diagonal AC =24 cm.
We know that diagonals of a rhombus bisect each other at right angles.
Therefore,Triangle AOB is a right-angled triangle, right angled at O.
\begin{array}{l} \Rightarrow AO = \frac {1}{2} \times AC=\frac {1}{2} \times 24=12 \text { cm and given that AD = 15 cm} \\ \text {Using Pythagoras theorem, we get} \\ (AD)^{2}=(AO)^{2}+(OD)^{2} \\ \Rightarrow \quad 15^{2}=12^{2}+ (OD)^{2} \\ \Rightarrow \quad (OD)^{2} = 15^{2} – 12^{2} \\ \Rightarrow \quad (OD)^{2} = 225 – 144 \\ \Rightarrow \quad (OD)^{2} = 81 \\ \Rightarrow \quad OD = \sqrt {9 \times 9} \\ \Rightarrow \quad OD = 9 \text { cm} \\\text {BD} = 2 \times OD = 2 \times 9 \text { cm} = 18 \text { cm} \\ \text {We know that area of rhombus ABCD}= \frac {1}{2}(\text {Product of the diagonals}) \\ \Rightarrow \quad \text {Area of rhombus ABCD}= \frac {1}{2}(24 \times 18) =216 \text { cm}^{2}\end{array}Q12. Find the area of a rhombus, each side of which measures 20 cm and one of whose diagonals is 24 cm.
Sol.

Let ABCD be the rhombus where diagonals intersect at O.
Given that side of rhombus = 20 cm.
And the diagonal AC = 24 cm.
We know that diagonals of a rhombus bisect each other at right angles.
Therefore,Triangle AOB is a right-angled triangle, right angled at O.
\begin{array}{l} \Rightarrow AO = \frac {1}{2} \times AC=\frac {1}{2} \times 24=12 \text { cm and given that AD = 20 cm} \\ \text {Using Pythagoras theorem, we get} \\ (AD)^{2}=(AO)^{2}+(OD)^{2} \\ \Rightarrow \quad 20^{2}=12^{2}+ (OD)^{2} \\ \Rightarrow \quad (OD)^{2} = 20^{2} – 12^{2} \\ \Rightarrow \quad (OD)^{2} = 400 – 144 \\ \Rightarrow \quad (OD)^{2} = 256 \\ \Rightarrow \quad OD = \sqrt {16 \times 16} \\ \Rightarrow \quad OD = 16 \text { cm} \\\text {BD} = 2 \times OD = 2 \times 16 \text { cm} = 32 \text { cm} \\ \text {We know that area of rhombus ABCD}= \frac {1}{2}(\text {Product of the diagonals}) \\ \Rightarrow \quad \text {Area of rhombus ABCD}= \frac {1}{2}(24 \times 32) =384 \text { cm}^{2}\end{array}Q13. The length of a side of a square field is 4 m. What will be the altitude of the rhombus, if the area of the rhombus is equal to the square field and one of its diagonals is 2 m?
Sol.

Given that the length of a side of a square field = 4 m.
Also given that, Area of the rhombus ABCD = Area of the square of side 4 m.
\begin{array}{l} \Rightarrow \quad \frac {1}{2} \times AC \times BD = 4^{2} \\ \Rightarrow \quad \frac {1}{2} \times AC \times 2 = 4^{2} \\ \Rightarrow \quad AC = 4^{2} = 16 \text { m} \\\text {We know that the diagonals of a rhombus are perpendicular bisectors of each other.} \\ \therefore AO= \frac {1}{2} \times AC=\frac {1}{2} \times 16 =8 \text { m} \\\text {And BO } =\frac {1}{2} \times BD =\frac {1}{2} \times 2 =1 \text { m} \\\text {Using Pythagoras theorem, we have } \\ AO^{2}+BO^{2}=AB^{2} \\ \Rightarrow \quad AB^{2}=8^{2}+ 1^{2} \\ \Rightarrow \quad AB^{2}=64+ 1 \\ \Rightarrow \quad AB^{2}=65 \\ \Rightarrow \quad AB=\sqrt{65} \text { m} \\\text {Area of the rhombus ABCD}= \frac {1}{2} \times AC \times BD \\ = \frac {1}{2} \times 16 \times 2 = 16 \text { m}^{2} \\\text {Also, we can calculate area of the rhombus ABCD} = \text {Base AB} \times \text {Altidude DL} \\ =\sqrt{65} \times DL \text { m}^{2} \\\Rightarrow \quad \sqrt{65} \times DL = 16 \\ \Rightarrow \quad DL = \frac {16}{\sqrt{65}} \text { m} \\\text {Hence, the altitude of the rhombus is } \frac {16}{\sqrt{65}} \text { m}\end{array}Q14. Two sides of a parallelogram are 20 cm and 25 cm. If the altitude corresponding to the sides of length 25 cm is 10 cm, find the altitude corresponding to the other pair of sides.
Sol.

ABCD is a parallelogram with longer side AB = 25 cm and corresponding altitude is DL = 10 cm.
Shorter side is BC = 20 cm and the corresponding altitude is DM.
Area of a parallelogram = Base × Height
\begin{array}{l} \Rightarrow \quad AB \times DL = BC \times DM \\ \Rightarrow \quad 25 \times 10 = 20 \times DM \\ \Rightarrow \quad DM = \frac {25 \times 10}{20} \\ \Rightarrow \quad DM = 12.5 \text { cm} \\ \end{array}Hence, the altitude corresponding to shorted side BC is 12.5 cm.
Q15. The base and corresponding altitude of a parallelogram are 10 cm and 12 cm respectively. If the other altitude is 8 cm, find the length of the other pair of parallel sides.
Sol.

ABCD is a parallelogram with side AB = 10 cm and corresponding altitude is DL = 12 cm.
Another side is BC and the corresponding altitude is DM having lenth 8 cm.
Area of a parallelogram = Base × Height
\begin{array}{l} \Rightarrow \quad AB \times DL = BC \times DM \\ \Rightarrow \quad 10 \times 12 = BC \times 8 \\ \Rightarrow \quad BC = \frac {10 \times 12}{8} \\ \Rightarrow \quad BC = 15 \text { cm} \\\end{array} Hence, lenth of side BC is 15 cm.
Q16. A floral design on the floor of a building consists of 280 tiles. Each tile is in the shape of a parallelogram of altitude 3 cm and base 5 cm. Find the cost of polishing the design at the rate of 50 paise per square cm.
Sol.
Given altitude of a tile = 3 cm.
Base of a tile = 5 cm.
$$ \text {Area of one tile }= \text {Attitude} \times \text {Base}=5 \times 3 \text { cm}^{2} $$ $$ =15 \text { cm}^{2} $$ $$ \text {Area of 280 tiles }=280 \times 15 = 4200 \text { cm}^{2} $$ $$ \text {Rate of polishing the tile }=\text {Rs. }0.5 per \text { cm}^{2} $$ Therefore, Total cost of polishing the design =4200 × 0.5= Rs. 2100
Sol.
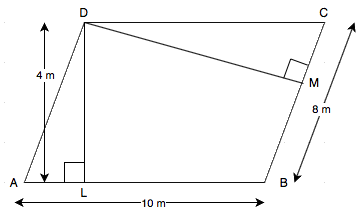
ABCD is a parallelogram with side AB = 10 m.
And corresponding altitude DL =4 m.
The adjacent side is BC = 8 m.
And the corresponding altitude is DM.
We know that area of a parallelogram = Base × Height
$$ \Rightarrow \quad AB \times DL= BC \times DM $$ $$ \Rightarrow \quad 10 \times 4= 8 \times DM $$ $$ \Rightarrow \quad DM = \frac {10 \times 4}{8} $$ $$ \Rightarrow \quad DM = 5 \text { m} $$ Hence, the distance between the shorter sides is 5 m.
Q10. The base of a parallelogram is twice its height. If the area of the parallelogram is 512 sq cm, find the base and height.
Sol.
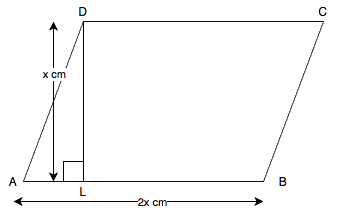
Let’s assume that height of the parallelogram be x cm.
Then given that base of the parallelogram is 2x cm. \begin{array}{l} \text {Also given that area of the parallelogram }=512 \text { cm}^{2} \\ \text {We know that area of a parallelogram }= \text {Base} \times \text {Height} \\ \Rightarrow \quad 512= 2x \times x \\ \Rightarrow \quad 2 x^{2}= 512\\ \Rightarrow \quad x^{2}= \frac {512}{2}\\ \Rightarrow \quad x^{2}= 256 \\ \Rightarrow \quad x= \sqrt {16 \times 16} \\ \Rightarrow \quad x= 16 \text { cm} \\ \text {Hence height of parallelogram }=x=16 \text { cm} \\ \text {And so base of the parallelogram }=2x=2 \times 16=32 \text { cm} \end{array}Q11. Find the area of a rhombus having each side equal to 15 cm and one of whose diagonals is 24 cm.
Sol.
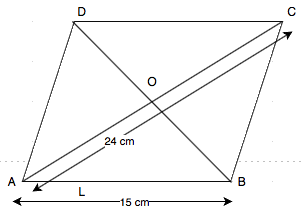
Let ABCD be the rhombus where diagonals intersect at O.
Given that side of rhombus =15 cm.
And the diagonal AC =24 cm.
We know that diagonals of a rhombus bisect each other at right angles.
Therefore,Triangle AOB is a right-angled triangle, right angled at O.
\begin{array}{l} \Rightarrow AO = \frac {1}{2} \times AC=\frac {1}{2} \times 24=12 \text { cm and given that AD = 15 cm} \\ \text {Using Pythagoras theorem, we get} \\ (AD)^{2}=(AO)^{2}+(OD)^{2} \\ \Rightarrow \quad 15^{2}=12^{2}+ (OD)^{2} \\ \Rightarrow \quad (OD)^{2} = 15^{2} – 12^{2} \\ \Rightarrow \quad (OD)^{2} = 225 – 144 \\ \Rightarrow \quad (OD)^{2} = 81 \\ \Rightarrow \quad OD = \sqrt {9 \times 9} \\ \Rightarrow \quad OD = 9 \text { cm} \\\text {BD} = 2 \times OD = 2 \times 9 \text { cm} = 18 \text { cm} \\ \text {We know that area of rhombus ABCD}= \frac {1}{2}(\text {Product of the diagonals}) \\ \Rightarrow \quad \text {Area of rhombus ABCD}= \frac {1}{2}(24 \times 18) =216 \text { cm}^{2}\end{array}Q12. Find the area of a rhombus, each side of which measures 20 cm and one of whose diagonals is 24 cm.
Sol.
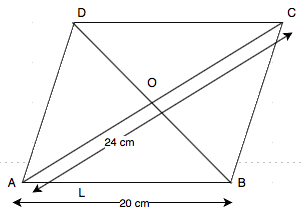
Let ABCD be the rhombus where diagonals intersect at O.
Given that side of rhombus = 20 cm.
And the diagonal AC = 24 cm.
We know that diagonals of a rhombus bisect each other at right angles.
Therefore,Triangle AOB is a right-angled triangle, right angled at O.
\begin{array}{l} \Rightarrow AO = \frac {1}{2} \times AC=\frac {1}{2} \times 24=12 \text { cm and given that AD = 20 cm} \\ \text {Using Pythagoras theorem, we get} \\ (AD)^{2}=(AO)^{2}+(OD)^{2} \\ \Rightarrow \quad 20^{2}=12^{2}+ (OD)^{2} \\ \Rightarrow \quad (OD)^{2} = 20^{2} – 12^{2} \\ \Rightarrow \quad (OD)^{2} = 400 – 144 \\ \Rightarrow \quad (OD)^{2} = 256 \\ \Rightarrow \quad OD = \sqrt {16 \times 16} \\ \Rightarrow \quad OD = 16 \text { cm} \\\text {BD} = 2 \times OD = 2 \times 16 \text { cm} = 32 \text { cm} \\ \text {We know that area of rhombus ABCD}= \frac {1}{2}(\text {Product of the diagonals}) \\ \Rightarrow \quad \text {Area of rhombus ABCD}= \frac {1}{2}(24 \times 32) =384 \text { cm}^{2}\end{array}Q13. The length of a side of a square field is 4 m. What will be the altitude of the rhombus, if the area of the rhombus is equal to the square field and one of its diagonals is 2 m?
Sol.
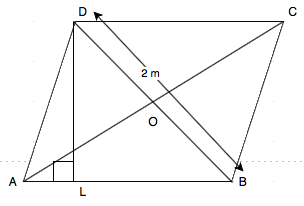
Given that the length of a side of a square field = 4 m.
Also given that, Area of the rhombus ABCD = Area of the square of side 4 m.
\begin{array}{l} \Rightarrow \quad \frac {1}{2} \times AC \times BD = 4^{2} \\ \Rightarrow \quad \frac {1}{2} \times AC \times 2 = 4^{2} \\ \Rightarrow \quad AC = 4^{2} = 16 \text { m} \\\text {We know that the diagonals of a rhombus are perpendicular bisectors of each other.} \\ \therefore AO= \frac {1}{2} \times AC=\frac {1}{2} \times 16 =8 \text { m} \\\text {And BO } =\frac {1}{2} \times BD =\frac {1}{2} \times 2 =1 \text { m} \\\text {Using Pythagoras theorem, we have } \\ AO^{2}+BO^{2}=AB^{2} \\ \Rightarrow \quad AB^{2}=8^{2}+ 1^{2} \\ \Rightarrow \quad AB^{2}=64+ 1 \\ \Rightarrow \quad AB^{2}=65 \\ \Rightarrow \quad AB=\sqrt{65} \text { m} \\\text {Area of the rhombus ABCD}= \frac {1}{2} \times AC \times BD \\ = \frac {1}{2} \times 16 \times 2 = 16 \text { m}^{2} \\\text {Also, we can calculate area of the rhombus ABCD} = \text {Base AB} \times \text {Altidude DL} \\ =\sqrt{65} \times DL \text { m}^{2} \\\Rightarrow \quad \sqrt{65} \times DL = 16 \\ \Rightarrow \quad DL = \frac {16}{\sqrt{65}} \text { m} \\\text {Hence, the altitude of the rhombus is } \frac {16}{\sqrt{65}} \text { m}\end{array}Q14. Two sides of a parallelogram are 20 cm and 25 cm. If the altitude corresponding to the sides of length 25 cm is 10 cm, find the altitude corresponding to the other pair of sides.
Sol.
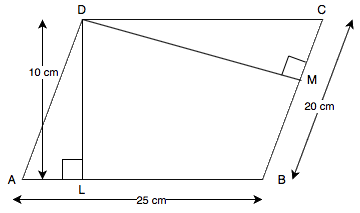
ABCD is a parallelogram with longer side AB = 25 cm and corresponding altitude is DL = 10 cm.
Shorter side is BC = 20 cm and the corresponding altitude is DM.
Area of a parallelogram = Base × Height
\begin{array}{l} \Rightarrow \quad AB \times DL = BC \times DM \\ \Rightarrow \quad 25 \times 10 = 20 \times DM \\ \Rightarrow \quad DM = \frac {25 \times 10}{20} \\ \Rightarrow \quad DM = 12.5 \text { cm} \\ \end{array}Hence, the altitude corresponding to shorted side BC is 12.5 cm.
Q15. The base and corresponding altitude of a parallelogram are 10 cm and 12 cm respectively. If the other altitude is 8 cm, find the length of the other pair of parallel sides.
Sol.

ABCD is a parallelogram with side AB = 10 cm and corresponding altitude is DL = 12 cm.
Another side is BC and the corresponding altitude is DM having lenth 8 cm.
Area of a parallelogram = Base × Height
\begin{array}{l} \Rightarrow \quad AB \times DL = BC \times DM \\ \Rightarrow \quad 10 \times 12 = BC \times 8 \\ \Rightarrow \quad BC = \frac {10 \times 12}{8} \\ \Rightarrow \quad BC = 15 \text { cm} \\\end{array} Hence, lenth of side BC is 15 cm.
Q16. A floral design on the floor of a building consists of 280 tiles. Each tile is in the shape of a parallelogram of altitude 3 cm and base 5 cm. Find the cost of polishing the design at the rate of 50 paise per square cm.
Sol.
Given altitude of a tile = 3 cm.
Base of a tile = 5 cm.
$$ \text {Area of one tile }= \text {Attitude} \times \text {Base}=5 \times 3 \text { cm}^{2} $$ $$ =15 \text { cm}^{2} $$ $$ \text {Area of 280 tiles }=280 \times 15 = 4200 \text { cm}^{2} $$ $$ \text {Rate of polishing the tile }=\text {Rs. }0.5 per \text { cm}^{2} $$ Therefore, Total cost of polishing the design =4200 × 0.5= Rs. 2100
