Q13. The radius of a circle is 14 cm. Find the radius of the circle whose area is double of the area of the circle.\begin{array}{l}
\text {Sol. Area of circle with radius 14 cm } = \pi (14)^{2} \text { cm}^{2} \\
\text {Area of new circle is double the area of first circle } =2 \times \pi (14)^{2} \text { cm}^{2} \\
\text {Lets assume that x cm be the radius of new circle.} \\
\therefore \text {Area of new circle with x cm radius} = \pi x^{2} \text { cm}^{2} \\
\Rightarrow \pi x^{2} = 2 \times \pi (14)^{2} \\
\Rightarrow x^{2} = 2 \times (14)^{2} \\
\Rightarrow x = 14 \sqrt {2} \text { cm} \\\text {Hence the radius of the new circle is } 14 \sqrt{2} \text { cm} \\
\end{array}Q14. The radius of one circluar field is 20 m and that of another is 48 m. Find the radius of the third circular field whose area is equal to the sum of the areas of two fields.\begin{array}{l}
\text {Sol. Area of circle having radius 20 metre is } A_{1} = \pi (20)^{2} \text { m}^{2} \\
\text {Area of circle having radius 48 metre is } A_{2} = \pi (48)^{2} \text { m}^{2} \\
\text {Given that Area of third circle having radius r metre } = A_{1} + A_{2} \\
\Rightarrow \pi r^{2} = [\pi (20)^{2} + \pi (48)^{2}] \\
\Rightarrow \pi r^{2} = \pi [(20)^{2} + \pi (48)^{2}] \\
\Rightarrow r^{2} = (400 + 2304) \\
\Rightarrow r^{2} = 2704 \\
\Rightarrow r = \sqrt {2704} \\
\Rightarrow r = 52 \text { m} \\\text {Hence, the radius of 3rd circle is 52 m.}
\end{array}Q15. The radius of one circular field is 5 m and that of the other is 13 m. Find the radius of the circular field whose area is the difference of the areas of first and second field.\begin{array}{l}
\text {Sol. Area of circular field having radius 5 metre is } A_{1} = \pi (3)^{2} \text { m}^{2} \\
\text {Area of circular field having radius 13 metre is } A_{2} = \pi (13)^{2} \text { m}^{2} \\
\text {Given that Area of circular field having radius r metre } = A_{2} – A_{1} \\
\Rightarrow \pi r^{2} = [\pi (13)^{2} – \pi (5)^{2}] \\
\Rightarrow \pi r^{2} = \pi [(13)^{2} – \pi (5)^{2}] \\
\Rightarrow r^{2} = (169 – 25) \\
\Rightarrow r^{2} = 144 \\
\Rightarrow r = \sqrt {144} \\
\Rightarrow r = 12 \text { m} \\\text {Hence, the radius of circular field is 12 m.}
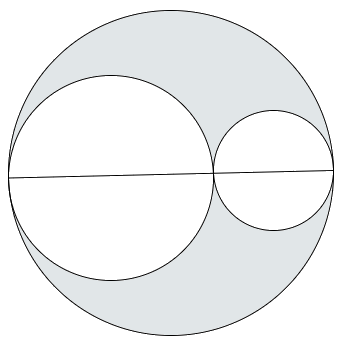
\end{array}Q16. Two circles are drawn inside a big circle with diameters ⅔ rd and ⅓ rd of the diameter of the big circle as shown in Fig. Find the area of the shaded portion, if the length of the diameter of the circle is 18 cm.

\begin{array}{l} \text {Sol. Given that the diameter of the big circle} =18 \text { cm} \\ \Rightarrow \text {Radius of the big circle } =\frac {18}{2} =9 \text { cm} \\ \text {Area of the big circle (A)}=\pi(9)^{2}=81 \pi \text { cm}^{2} \\ \text {Diameter of first inner circle }= \frac {2}{3} \times \text {Diameter of big outside circle} \\ = \frac {2}{3} \times 18 = 12 \text { cm} \\ \Rightarrow \text {Radius first inner circle } r_{1} = \frac {12}{2} = 6 \text { cm} \\ \text {Area of first inner circle with radius 6 cm } A_{1} = \pi (6)^{2} = 36 \pi \text { cm}^{2} \\\text {Diameter of second inner circle }= \frac {1}{3} \times \text {Diameter of big outside circle} \\ = \frac {1}{3} \times 18 = 6 \text { cm} \\ \Rightarrow \text {Radius first inner circle } r_{2} = \frac {6}{2} = 3 \text { cm} \\ \text {Area of second inner circle with radius 3 cm } A_{2} = \pi (3)^{2} = 9 \pi \text { cm}^{2} \\\therefore \text {Area of the shaded portion} =A- A_{1} – A_{2} \\ =81 \pi- 36 \pi – 9 \pi =36 \pi \text { cm}^{2} \\ \end{array}Q17. In Fig., the radius of quarter circular plot taken is 2 m and radius of the flower bed is 2 m. Find the area of the remaining field.

\begin{array}{l} \text {Sol. Given that Radius of flower bed} =2 \text { m} \\ \text {Area of flower bed } =\pi r^{2}=\pi(2)^{2}=4 \pi \text { m}^{2} \\ \text {Radius of the quarter circular plot } =2 \text { m} \\ \text {Area of the quarter circular plot with radius 2 m } =\frac {\pi r^{2}}{4} \text { m}^{2} \\ = \frac {\pi (2)^{2}}{4} \text { m}^{2} \\ = \pi \text { m}^{2} \\\text {Area of 4 quarter circular plots } =4 \times \pi \text { m}^{2} = 4 \pi \text { m}^{2} \\\text {We know that area of the rectangular} = \text {Length} \times \text {Breadth} \\ =8 \times 6 =48 \text { m}^{2} \\\text {Required area of the remaining field } \\ = \text {Area of the rectangule} – \text {Area of 4 quarter circular plots} – \text {Area of the flower bed} \\ =48- 4 \pi – 4 \pi \\ = 48 – 8 \times \frac {22}{7} \\ =48-25.14 =22.86 \text { m}^{2} \\\end{array}Q18. Four equal circles, each of radius 5 cm, touch each other as shown in Fig. Find the area included between them. (Take) π =3.14

\begin{array}{l} \text {Sol. From the givne figure, we can conclude clearly that Side of the square }=10 \text { cm} \\ \therefore \text {Area of the square } =(\text {Side})^{2}=10 \times 10=100 \text { cm}^{2} \\ \text {Area of the four quarter circles }= 4 \times \frac {\pi r^{2}}{4} \\ =4 \times \frac{1}{4} \times \frac{22}{7} \times 5^{2} \\ =78.57 \text { cm}^{2} \\\text {Hence, required area } = \text {Area of the square} – \text {Area of the four quarter circles} \\ =(100-78.57) \text { cm}^{2} \\ =21.43 \text { cm}^{2} \\ \end{array}Q19. The area of circle is 100 times the area of another circle. What is the ratio of their circumferences?
\begin{array}{l} \text {Sol. Lets assume that the area of the circles be } A_{1} \text { and } A_{2} \text { and their circumference be } \\ c_{1} \text { and } c_{2} \text {respectively.} \\ \text {Also } r_{1} \text { and } r_{2} \text { are their respective radius} \\\text {According to the question, we have } \\ A_{1}=100 A_{2} \\ \Rightarrow \pi r_{1}^{2} =100 \times \pi r_{2}^{2} \\ \Rightarrow \frac {r_{1}^{2}}{r_{2}^{2}} = \frac {100}{1} \\ \Rightarrow \frac {r_{1}}{r_{2}} = \sqrt {\frac {100}{1}} \\ \Rightarrow \frac {r_{1}}{r_{2}} = \frac {10}{1} \\\text {Ratio of circumference} \\ C_{1} : C_{2} = \frac { C_{1}}{ C_{2}} \\ = \frac {2 \pi r_{1}}{ 2 \pi r_{2}} \\ = \frac {r_{1}}{r_{2}} \\ = \frac {10}{1} \\\text {Hence } C_{1} : C_{2} = 10 : 1 \\ \end{array}
\begin{array}{l} \text {Sol. Given that the diameter of the big circle} =18 \text { cm} \\ \Rightarrow \text {Radius of the big circle } =\frac {18}{2} =9 \text { cm} \\ \text {Area of the big circle (A)}=\pi(9)^{2}=81 \pi \text { cm}^{2} \\ \text {Diameter of first inner circle }= \frac {2}{3} \times \text {Diameter of big outside circle} \\ = \frac {2}{3} \times 18 = 12 \text { cm} \\ \Rightarrow \text {Radius first inner circle } r_{1} = \frac {12}{2} = 6 \text { cm} \\ \text {Area of first inner circle with radius 6 cm } A_{1} = \pi (6)^{2} = 36 \pi \text { cm}^{2} \\\text {Diameter of second inner circle }= \frac {1}{3} \times \text {Diameter of big outside circle} \\ = \frac {1}{3} \times 18 = 6 \text { cm} \\ \Rightarrow \text {Radius first inner circle } r_{2} = \frac {6}{2} = 3 \text { cm} \\ \text {Area of second inner circle with radius 3 cm } A_{2} = \pi (3)^{2} = 9 \pi \text { cm}^{2} \\\therefore \text {Area of the shaded portion} =A- A_{1} – A_{2} \\ =81 \pi- 36 \pi – 9 \pi =36 \pi \text { cm}^{2} \\ \end{array}Q17. In Fig., the radius of quarter circular plot taken is 2 m and radius of the flower bed is 2 m. Find the area of the remaining field.

\begin{array}{l} \text {Sol. Given that Radius of flower bed} =2 \text { m} \\ \text {Area of flower bed } =\pi r^{2}=\pi(2)^{2}=4 \pi \text { m}^{2} \\ \text {Radius of the quarter circular plot } =2 \text { m} \\ \text {Area of the quarter circular plot with radius 2 m } =\frac {\pi r^{2}}{4} \text { m}^{2} \\ = \frac {\pi (2)^{2}}{4} \text { m}^{2} \\ = \pi \text { m}^{2} \\\text {Area of 4 quarter circular plots } =4 \times \pi \text { m}^{2} = 4 \pi \text { m}^{2} \\\text {We know that area of the rectangular} = \text {Length} \times \text {Breadth} \\ =8 \times 6 =48 \text { m}^{2} \\\text {Required area of the remaining field } \\ = \text {Area of the rectangule} – \text {Area of 4 quarter circular plots} – \text {Area of the flower bed} \\ =48- 4 \pi – 4 \pi \\ = 48 – 8 \times \frac {22}{7} \\ =48-25.14 =22.86 \text { m}^{2} \\\end{array}Q18. Four equal circles, each of radius 5 cm, touch each other as shown in Fig. Find the area included between them. (Take) π =3.14

\begin{array}{l} \text {Sol. From the givne figure, we can conclude clearly that Side of the square }=10 \text { cm} \\ \therefore \text {Area of the square } =(\text {Side})^{2}=10 \times 10=100 \text { cm}^{2} \\ \text {Area of the four quarter circles }= 4 \times \frac {\pi r^{2}}{4} \\ =4 \times \frac{1}{4} \times \frac{22}{7} \times 5^{2} \\ =78.57 \text { cm}^{2} \\\text {Hence, required area } = \text {Area of the square} – \text {Area of the four quarter circles} \\ =(100-78.57) \text { cm}^{2} \\ =21.43 \text { cm}^{2} \\ \end{array}Q19. The area of circle is 100 times the area of another circle. What is the ratio of their circumferences?
\begin{array}{l} \text {Sol. Lets assume that the area of the circles be } A_{1} \text { and } A_{2} \text { and their circumference be } \\ c_{1} \text { and } c_{2} \text {respectively.} \\ \text {Also } r_{1} \text { and } r_{2} \text { are their respective radius} \\\text {According to the question, we have } \\ A_{1}=100 A_{2} \\ \Rightarrow \pi r_{1}^{2} =100 \times \pi r_{2}^{2} \\ \Rightarrow \frac {r_{1}^{2}}{r_{2}^{2}} = \frac {100}{1} \\ \Rightarrow \frac {r_{1}}{r_{2}} = \sqrt {\frac {100}{1}} \\ \Rightarrow \frac {r_{1}}{r_{2}} = \frac {10}{1} \\\text {Ratio of circumference} \\ C_{1} : C_{2} = \frac { C_{1}}{ C_{2}} \\ = \frac {2 \pi r_{1}}{ 2 \pi r_{2}} \\ = \frac {r_{1}}{r_{2}} \\ = \frac {10}{1} \\\text {Hence } C_{1} : C_{2} = 10 : 1 \\ \end{array}
